Materialism Is Not Enough

Kurt Gödel: Logic, Rationalism, and Materialism

I have been hammering secular materialism (“rationalism” / “physicalism”) as of late:

I will continue to do so until spiritual morale improves.

Today, we continue this much needed trend. But this time, by using the materialist’s best logician, Kurt Gödel.

Gödel was a genius and one of my favorite philosophers to study. He was a mathematician and a logician during the height of post-Enlightenment rationalism.

Here is a quick summary:

Kurt Friedrich Gödel (German: April 28, 1906 – January 14, 1978) was a logician, mathematician, and philosopher. Considered along with Aristotle and Gottlob Frege to be one of the most significant logicians in history, Gödel had an immense effect upon scientific and philosophical thinking in the 20th century, a time when others such as Bertrand Russell, Alfred North Whitehead, and David Hilbert were using logic and set theory to investigate the foundations of mathematics, building on earlier work by the likes of Richard Dedekind, Georg Cantor and Frege.

Gödel, a product of the era of rational materialism, used his own field of mathematics/logic to prove that logic cannot prove everything.

He did so most famously with the incompleteness theorems.

These theorems, in simple terms, can be found here:

First incompleteness theorem: Any consistent formal system F within which a certain amount of elementary arithmetic can be carried out is incomplete; i.e., there are statements of the language of F which can neither be proved nor disproved in F.
Second incompleteness theorem: For any consistent system F within which a certain amount of elementary arithmetic can be carried out, the consistency of F cannot be proved in F itself.

While I am forced to shorten the mathematics and analysis behind the theorems due to the desire to not alienate 90% of my readers, I fully implore all of my readers to really dive into the two theorems if they can. They are a treasure trove of insight, sitting out in the open for whoever is willing to put in the time to understand them.

Those two simple theories revolutionized our understanding of the limitations of logical analysis.

A good article that explains why they did so is here:

Kurt Gödel’s Incompleteness Theorems and Philosophy
In 1930, Kurt Gödel shocked the mathematical world when he delivered his two Incompleteness Theorems. These theorems , which we will explain shortly, uncovered a fundamental truth about the nature of mathematics, a truth that the majority of the mathematicians back in the day were not ready to accept.
[…]
First Incompleteness Theorem
Every mathematical system, powerful enough to describe computation is either incomplete or inconsistent.
Second Incompleteness Theorem
A consistent mathematical system cannot prove its own consistency.
[…]
Okay, now let’s brake these theorems down starting with the first one.
First of all, the “powerful enough to describe computation” — or “sufficiently expressive” as it is sometimes called — should not scare us. Loosely speaking, the majority of mathematical systems that we non-mathematicians are concerned about have this property. We will not dive into this much more since it not important for our understanding.
With the above remark in mind, the first of our two theorems tells us that every system that we have in our disposal is either incomplete or inconsistent. That means, that there are either some true statements in our system that we will never be able to prove or that our system contradicts itself (inconsistent). As we have previously stated, we do not want our systems to be inconsistent so we are left to hope that they are incomplete. The use of the word “hope” in the previous sentence is not random. We would like to have a way to prove that our system is actually incomplete and not inconsistent but Gödel’s second theorem now comes into play and deprives us of that possibility.
However, since we haven’t yet come across any inconsistencies we pretty much take it for granted that our systems are consistent but incomplete. Let’s ponder over what that entails for a minute.
What we just admitted is that there are some deep fundamental truths about mathematics and our universe, in general, that we will never be able to uncover. Reality is not “logically incomplete”. We are just not equipped with the right tools, yet, to fully understand it. It is not a matter of intelligence or mathematical skill. We are not waiting for the next Euler or Gauss to come in our aid. It is simply not possible. One fairly common recommendation of a person that hears about this revelation for the first time is to add the “unprovable” statements as axioms in our systems. However, this is of no use since by the addition of more axioms we give birth to a brand new mathematical system which is still subject to the two Incompleteness Theorems. There is no way out.
The philosophical implications of the Incompleteness Theorems are tremendous. To our knowledge, there is not another theorem in the mathematical world that can match the turmoil that Gödel’s work created when first published. Mathematicians who had devoted their entire lives to the pursuit for a proof of certain mathematical statements were now faced with the possibility that all of their lives’ work was in vain. A question kept popping up in every mathematician’s mind when he was deciding whether or not to tackle a new problem: “What if it cannot be proven?”.

The most important piece out of that quote is this part:

What we just admitted is that there are some deep fundamental truths about mathematics and our universe, in general, that we will never be able to uncover. Reality is not “logically incomplete”. We are just not equipped with the right tools, yet, to fully understand it. It is not a matter of intelligence or mathematical skill. We are not waiting for the next Euler or Gauss to come in our aid. It is simply not possible.

One of the world’s greatest rationalists used rationalism to prove the questions of the universe are irreconcilably unsolvable by rationalism alone.

The ramifications of this are still lingering today, and millions of people still are blind to this reality.

But he didn’t stop there. Once broken from the chains of rationalism, Gödel went on to study “intuition”—a term we will use later. This lead him to create Gödel’s ontological proof, which was a mathematical proof that God exists (using “intuition” for God in the form of a godlike object). An easy-to-understand breakdown of that proof can be found here.

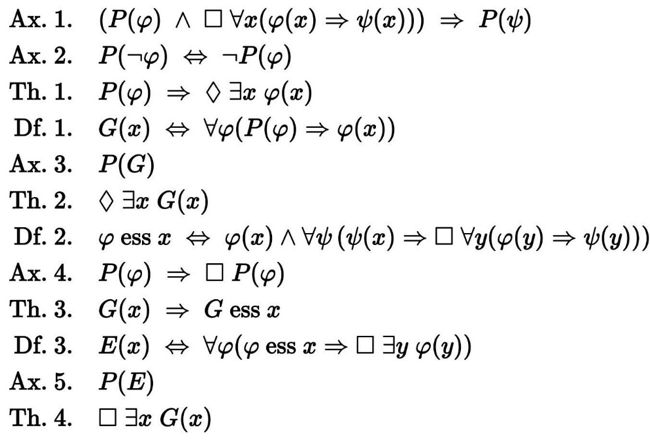
Kurt Gödel’s ontological proof on the existence of God

There is a documentary called “Dangerous Knowledge” that is decent as an introduction to Gödel, but they don’t really get to the heart of the matter as much as I would prefer. It does provide a high level sufficient overview, however. It also connects him to Turing, an essential piece to understanding the core materialist beliefs.

That documentary can be found on Daily Motion:

In this one-off documentary, David Malone looks at four brilliant mathematicians – Georg Cantor, Ludwig Boltzmann, Kurt Gödel and Alan Turing – whose genius has profoundly affected us, but which tragically drove them insane and eventually led to them all committing suicide. The film begins with Georg Cantor, the great mathematician whose work proved to be the foundation for much of the 20th-century mathematics. He believed he was God’s messenger and was eventually driven insane trying to prove his theories of infinity.

This documentary explores the connection between the ideas of Gödel and Turing on what Gödel’s incompleteness means for us. It demonstrates the limitations of any universal rationalist hypothesis.

The point is simple:

Rationalism can only get us so far. And that isn’t very far at all, relative to all (infinity).

Luckily, we’re not stuck with just that one form, as the secular materialists would have you believe.

You also have both intuition and the Spirit.

We are in the image of the triune God, with three parts of our own. While not necessarily sharing the three persons aspect of the greater Divine, we do have three noticeable (intuitive) elements: mind, soul, and spirit.

These three are distinct. There are few people that would argue that their soul is not often at war with their mind. Drug addicts are a clear example. Many of them crave freedom from addiction from deep within their soul, while the mind craves further usage.

To only rely on one of those faculties (the mind) is a degeneration. Use your soul and spirit, or walk blindly.

The Spirit is obvious. It is God, and the divine revelation in the world shown to all men. Read Romans 1:18-23. The Holy Spirit is one conduit for this.

Intuition is the “gut”, the intrinsic understanding of your connection with the spiritual realm that can lead you and help you perceive things with foreknowledge.

My goal in this article is to convince you to use all three.

To neglect none.

When you walk through a black neighborhood in downtown Memphis at night, it is not rationalism that is speaking to you. You don’t put on your nerd glasses and go “gee-wiz, blacks have an x% disproportionally higher crime rate, and this seems like an impoverished area which would contribute to a potential negative action against me“. No, you just know it is dangerous. You can feel it. You all know this, you’ve had it at some point. That is your intuition.

Or if you’re a Christian, it’s also the Spirit telling you that you’re an idiot and to turn back. You’re not crunching data numbers or thinking about statistical probability. That’s why even leftists—who reject that rationalist conclusion—know dangerous areas. To deny we have this is to deny an obvious reality.

Many Christians don’t seem to properly recognize that we literally have God with us. He is actually there, sitting with you right now. To then assume that your rationalism is the highest form is a spit in his face. It is a complete inversion.

We can, and should, use the data (rationalism) to confirm the intuition and workings of the spirit. But note the order. One starts with the spirit, the other with the material.

To reject modernity is to reject its foundational epistemological philosophy: rationalism. And to return to the proper form, the form that all of Western Civilization used throughout our entire history (Yes, including the Greco-Roman era). Which was to start with the Spirit or intuition, and then to use rationalism to dig deeper.

This is why theology is classically defined as “faith seeking understanding”. We start with the Spirit. We start with intuition. Finally, we then use the mind to further our understanding of that reality.

We intuitively know that there is a problem with clown world. We do not need data to prove it. But the data can assist us in furthering our understanding of why it is wicked. Likewise, we know that beauty exists (such as in inspiring ancient architecture compared to repulsive modern architecture) from the Spirit. But discursive reasoning can help us uncover aspects of what is true and beautiful, along with why.

This is the proper pathway to true wisdom. And to truth itself. We start with the spiritual, and then seek further understanding.

If we attempt this process backwards, we get nowhere. Because, as Gödel proved, it is the most limited form. Because it is the purely physical, material form. Or, as God put it, “Professing to be wise, they became fools“.

That is the fundamental, irreconcilable flaw with modernity. One that traps as many leftist scientists as it does dissidents.

The spiritual form is higher than the physical form. We’ve switched those because of the “Enlightenment” mindset.

The job of the dissident is to break away from all aspects of modernity. There is perhaps no greater secession needed than this one, because this foundational pillar is what allows the rest. If you stay within the comfort of modernity’s core philosophical positions, you will never escape its stranglehold.

We have the mind—Use it. But don’t neglect the greater forms in the process.

If you enjoyed this article, bookmark the website and check back often for new content. New articles most weekdays.

You can also keep up with my writing by joining my monthly newsletter.

Help fight the censorship – Share this article!